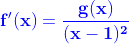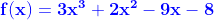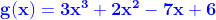Numerical function exercise 1.
I/ g is a numerical function defined on ℝ -{1} by: g(x)=x²-2x+ln |x-1|
1-Study the change of the function g And calculate g(0) and g(2).
2-Conclude the sign of g(x) According to the value of x.
II/ f is a numerical function defined on ℝ -{1} by:
and (c) Its graphic representation in a homogeneous and
orthogonal coordinate system (o;i⇀,j⇀) .
1-Prove that for every x of ℝ -{1} Then:
2-Prove that the curve (c) accepts two asymptotic lines, one of which is oblique (Δ), Then write an equation of (Δ).
3-Study the position of the curve (c) in relation to the straight line (Δ).
4-Prove that the curve (c) accepts two tangents (T) and (T') with the parallel of a straight
line (Δ), then write the equations of (T) and (T').
5- Prove that the point w(-1;1) is the center of symmetry of
the curve (c).
6- Prove that the curve (c) accept two inflection point, And select them.
7-Create the two tangents (T) and (T') and the curve (c).
8- h function defined on ℝ* by:
and (Ch) Its graphic representation in the previous coordinate system.
prove that (Ch) is the image of (C) by Translation. And draw it.
Numerical function exercise 2.
g is a function defined on ]0;+∞[ by: g(x)=x²-2+lnx
1- Study the change of the function g on ]0;+∞[ .
2-Prove that the equation accepts a single solution α Where:
1.31 < a < 1.32
3-Conclude the sign of g(x) on ]0;+∞[ .
II) We consider the function f defined on ]0;+∞[ by:
f(x)=x²+(2-lnx)²
2- conclude the change of the function f on ]0;+∞[ .
Numerical function exercise 3.
f is a Polynomial function where:
1-Calculate f(-1) and then find the real numbers a , b, c
where:
f(x)=(x-1)(ax+bx+c)
2-numerical function defined on ℝ by:
and (D) straight line its equation y=2x+2
a) Prove that the curve (Cg) Representative of the function g and the straight line (D) They have a common point A its range is zero.
b) Calculate g'(x) and write the equation of the tangent of (Cg)
at the point A.
objectives:
The objective of the first exercise: Study the change of the function and determination
its sign; determination the derivative of a
function; determination asymptotic lines and the position of the curve in relation to the straight line; determination the center of symmetry of the curve; determination
the inflection point and Create the two
tangents; determination the translation of the curve.
The objective of the second exercise: Study the change of the function; Define an
restriction to solve the function; determination
its sign of the function; and conclude the change of the function from another function.
The objective of the third exercise: analysis Polynomial to two factors; and determine the point of
intersection of a curved with a straight line.
____________________________________________________________________________
Please wait 30 seconds